最近事情无比之多,换了工作、组队参加了一个比赛、和朋友搞了一些小项目,公号荒废许久。坚持是多么重要,又是多么艰难,目前事情都告一段落,我们继续100天搞定机器学习系列。想要继续做这个是因为,一方面在具体应用中,发现很多之前遗漏的点,可以在这里查漏补缺,巩固知识点。另一方面,也是想大家一起打卡学习,一起探讨。
那么,继续学习。

本算法很简单,day7,原文作者仅简单介绍了kNN算法。
01k-NN算法
K最近邻(k-Nearest Neighbor,KNN)是数据挖掘分类技术中最简单的方法之一,是机器学习中唯一一个不需要训练过程的算法。K最近邻,即每个样本都可以用它最近的k个邻居代表。核心思想是如果两个样本的特征足够相似,它们就有更高的概率属于同一个类别,并具有这个类别上样本的特性。比较通俗的说法就是“近朱者赤近墨者黑”。
优点是简单,易于理解,易于实现,无需估计参数,无需训练;适合对稀有事件进行分类;特别适合于多分类问题, kNN比SVM的表现要好。
缺点是算法复杂度高,每一个待分类的样本都要计算它到全体已知样本的距离,效率较低;预测结果不具有可解释性,无法给出像决策树那样的规则;
02KNN如何工作?
kNN算法的过程如下:
1、选择一种距离计算方式, 通过数据所有的特征计算新数据与已知类别数据集中数据点的距离;
2、按照距离递增次序进行排序, 选取与当前距离最小的 k 个点;
3、对于离散分类, 返回 k 个点出现频率最多的类别作为预测分类; 对于回归, 返回 k 个点的加权值作为预测值。

如上图中,对灰色圆点进行分类,划分其属于绿、黄、红何种类型。首先需要计算灰点和近邻电之间的距离,确定其k近邻点,使用周边数量最多的最近邻点类标签确定对象类标签,本例中,灰色圆点被划分为黄色类别。
03几种距离
距离越近,表示越相似。距离的选择有很多,通常情况下,对于连续变量, 选取欧氏距离作为距离度量; 对于文本分类这种非连续变量, 选取汉明距离来作为度量. 通常如果运用一些特殊的算法来作为计算度量, 可以显著提高 K 近邻算法的分类精度,如运用大边缘最近邻法或者近邻成分分析法。
欧氏距离
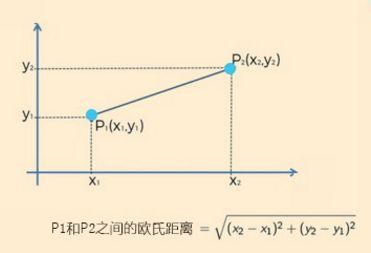
切比雪夫距离
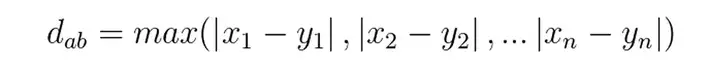
马氏距离
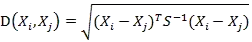
夹角余弦距离
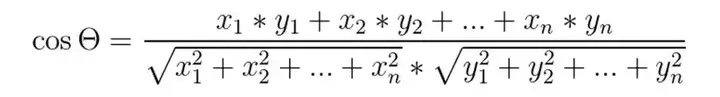
切比雪夫距离
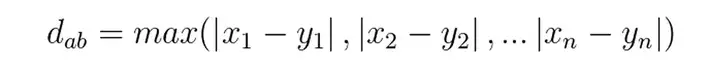
曼哈顿(Manhattan)距离
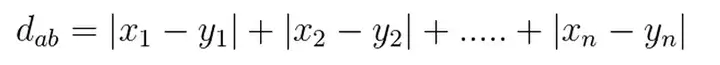
关于这些距离细节,大家可以移步:
https://blog.csdn.net/Kevin_cc98/article/details/73742037
https://blog.csdn.net/wyqwilliam/article/details/81676785
04K值
k值是可以直接影响预测结果的自定义常数。k值选择太小,邻居就会过少,易受噪声数据干扰,导致分类精度较低。k值选择太大,易蒋不相似数据包含进来,造成噪声增加,分类效果不佳。比较常用的是使用交叉验证误差统计选择法,比较不同K值时的交叉验证平均误差率, 选择误差率最小的那个K值. 例如选择K=1, 2, 3, ... , 对每个K = i 做100次交叉验证, 计算出平均误差, 通过比较选出误差最小的那个。
参考文献:https://baike.baidu.com/item/%E9%82%BB%E8%BF%91%E7%AE%97%E6%B3%95/1151153?fr=aladdinhttps://www.cnblogs.com/lijingchn/p/5398483.html
https://wenku.baidu.com/view/d84cf670a5e9856a561260ce.html